4  Лабораторна робота № 4

Тема. Інформаційні методи оцінки складності

Мета. Навчитися використовувати основні показники складності з теорії інформації для аналізу часових рядів

4.1 Теоретичні відомості

4.1.1 Складність. Кількісні міри складності. Інформаційні методи оцінки складності.

Дане століття називають століттям складності. Сьогодні питання “що таке складність?” вивчають фізики, біологи, математики і інформатики, хоча при теперішніх досягненнях у розумінні оточуючого світу, однозначної відповіді на це питання немає.

З цієї причини, відповідно до ідеї І. Пригожина, будемо досліджувати прояви складності системи, застосовуючи при цьому сучасні методи кількісного аналізу складності  [1].

Серед таких методів на увагу заслуговують:

• інформаційно-ентропійні;
• засновані на теорії хаосу;
• скейлінгово-мультифрактальні.

Зрозуміло, виходячи з різної природи методів, покладених в основу формування міри складності, вони приділяють певні вимоги до часових рядів, що слугують вхідними даними. Наприклад, перші дві групи методів вимагають стаціонарності вхідних даних. При цьому мають різну чутливість до таких характеристик, як детермінованність, стохастичність, причинність та кореляції. Тому у подальшому, порівнюючи комплексно ефективність різних показників складності, на вказані обставини ми будемо звертати увагу, підкреслюючи спеціально застосовність того чи іншого показника для характеристики різних сторін складності досліджуваних систем.

Розгляд першої групи методів почнемо з добре відомої міри складності, запропонованої А. Колмогоровим  [2].

Колмогорівська складність. Поняття колмогорівської складності (або, як ще говорять, алгоритмічної ентропії) з’явилося в 1960-і роки на стику теорії алгоритмів, теорії інформації і теорії ймовірностей.

Ідея А. Колмогорова полягала в тому, щоб вимірювати кількість інформації, що міститься в індивідуальних скінчених об’єктах (а не у випадкових величинах, як у шеннонівській теорії інформації). Виявилось, що це можливо (хоча лише з точністю до обмеженого доданку). А. Колмогоров запропонував вимірювати кількість інформації в скінчених об’єктах за допомогою теорії алгоритмів, визначивши складність об’єкту як мінімальну довжину програми, що породжує цей об’єкт. Дане визначення стало базисом алгоритмічної теорії інформації, а також алгоритмічної теорії ймовірностей: об’єкт вважається випадковим, якщо його складність наближена до максимальної.

Що ж собою являє колмогорівська складність і як її виміряти? На практиці ми часто стикаємося з програмами, які стискують файли (для економії місця в архіві). Найбільш поширені називаються zip, gzip, compress, rar, arj та інші. Застосувавши таку програму до деякого файлу (з текстом, даними, програмою), ми отримуємо його стислу версію (яка, як правило, коротше початкового файлу). За нею можна відновити початковий файл з допомогою парної програми — “декомпресора”. Отже, у першому наближенні колмогорівську складність файлу можна описати як довжину його стислої версії. Тим самим файл, що має регулярну структуру і добре стискуваний, має малу колмогорівську складність (порівняно з його довжиною). Навпаки, погано стискуваний файл має складність, близьку до довжини.

Припустимо, що ми маємо фіксований спосіб опису (декомпресор) $D$. Для даного слова $x$ розглянемо всі його описи, тобто всі слова $y$, для яких $D(y)$ визначене й рівне $x$. Довжину найкоротшого з них $l(y)$ і називають колмогорівською складністю слова $x$ при даному способі опису $D$:

$$K{S}_D(x)=min\{l(y)|D(y)=x\},$$

де $l(y)$ позначає довжину слова $y$. Індекс $D$ підкреслює, що визначення залежить від вибору способу $D$.

Можна показати, що існують оптимальні способи опису. Спосіб опису тим кращий, чим він коротший. Тому природно дати таке визначення: спосіб $D_1$ не гірше за спосіб $D_2$, якщо $K{S}_{D_1}(x)\le K{S}_{D_2}(x)+c$ при деякому $c$ і при всіх $x$.

Отже, за Колмогоровим, складність об’єкту (наприклад, тексту — послідовності символів) — це довжина мінімальної програми яка виводить даний текст, а ентропія — це складність, що ділиться на довжину тексту. Також можна розглядати алгоритмічну складність як мінімальний час (або інші обчислювальні ресурси), необхідний для виконання цієї задачі на комп’ютері. А ще ми можемо говорити про комунікаційну складність завдань, в яких задіяно більше одного процесора: це кількість бітів, які потрібно передати при розв’язанні цього завдання  [3,4]. На жаль, це визначення чисто умоглядне. Надійного способу однозначно визначити цю програму не існує. Але є алгоритми, які фактично якраз і намагаються обчислити колмогорівську складність тексту  [5] і ентропію  [6].

4.1.2 Оцінка складності Колмогорова за схемою Лемпела-Зіва

Універсальна (в сенсі застосовності до різних мовних систем) міра складності кінцевої символьної послідовності була запропонована Лемпелем і Зівом (Lempel and Ziv, LZ)  [7]. Складність Лемпеля-Зіва (Lempel-Ziv complexity, LZC) є класичною мірою, яка для ергодичних джерел пов’язує поняття складності (у розумінні Колмогорова-Чайтіна) та швидкості ентропії  [8,9]. Для ергодичного динамічного процесу кількість нової інформації, отриманої за одиницю часу (швидкість ентропії), може бути оцінена шляхом вимірювання здатності цього джерела генерувати нові патерни. Завдяки простоті методу LZC, швидкість ентропії може бути оцінена з однієї дискретної послідовності вимірювань з низькими обчислювальними витратами  [10]. У рамках їх підходу складність послідовності оцінюється числом кроків процесу, що її породжує. Припустимими (редакційними) операціями при цьому є:

1. Генерація символу (необхідна, як мінімум, для синтезу елементів алфавіту).
2. Копіювання “готового” фрагмента з передісторії (тобто з уже синтезованої частини тексту).

Нехай $\mathrm{\Sigma }$ — скінчений алфавіт, $S$ — текст (послідовність символів), складений з елементів $\mathrm{\Sigma }$; $S[i]$ — $i$-й символ тексту; $S[i:j]$ — фрагмент тексту з $i$-го по $j$-й символ включно $(i<j)$; $N=|S|$ — довжина тексту $S$. Тоді схему синтезу послідовності можна представити у вигляді конкатенації

$$\begin{array}{}\text{(4.1)}& H(S)=S[1:i_1]S[i_1+1:i_2]...S[i_{k-1}+1:i_k]...S[i_{m-1}+1:N],\end{array}$$

де $S[i_{k-1}+1:i_k]$ — фрагмент $S$, породжуваний на $k$-му кроці, а $m=m_H(S)$ — число кроків процесу. З усіляких схем породження $S$ обирається мінімальна за числом кроків. Таким чином, складність послідовності $S$ за LZ

$$c_{LZ}(S)=\underset{H}{min}\{m_H(S)\}.$$

Мінімальність числа кроків забезпечується вибором для копіювання на кожному кроці максимально довгого прототипу з передісторії. Якщо позначити через $j(k)$ номер позиції, з якої починається копіювання на $k$-му кроці, то довжина фрагмента копіювання

$$\begin{array}{}\text{(4.2)}& l_{j(k)}=i_k-i_{k-1}-1=\underset{j\le i_{k-1}}{max}\{l_j:S[i_{k-1}+1:i_{k-1}+l_j]=S[j:j+l_j-1]\},\end{array}$$

а сам $k$-й компонент складнісного розкладання (4.1) можна записати у вигляді

$$\begin{array}{}\text{(4.3)}& S[i_{k-1}+1:i_k]=\{\begin{array}{ll}S[j(k):j(k)+l_{j(k)}-1]& \text{якщо}j(k)\ne 0,\\ S[i_{k-1}+1]& \text{якщо}j(k)=0.\end{array}\end{array}$$

Випадок $j(k)=0$ відповідає ситуації, коли в позиції $i_{k-1}+1$ стоїть символ, який раніше не зустрічався. При цьому ми застосовуємо операцію генерації символу.

Будемо знаходити складність за LZ для часового ряду, який являє собою, наприклад, щоденні значення фінансового індексу. Для дослідження динаміки LZ та порівняння з іншими складними системами будемо знаходити дану міру складності для підряду фіксованої довжини (вікна). Для цього обчислимо логарифмічні прибутковості та перетворимо їх у послідовність бітів. При цьому можна задавати кількість станів, що диференційовані (система числення). Так, для двох різних станів маємо 0, 1, для трьох — 0, 1, 2 і т.д. Для двійкової системи кодування буде задаватися поріг по середньому значенню і стани, наприклад, прибутковостей (ret) кодуватимуться наступним чином  [11–13]:

$$\begin{array}{}\text{(4.4)}& ret=\{\begin{array}{ll}0,& re{t}_t<⟨ret⟩,\\ 1,& re{t}_t>⟨ret⟩.\end{array}\end{array}$$

Також можна визначити так звану пермутаційну складність Лемпеля-Зіва (permutation Lempel-Ziv complexity, PLZС)  [14,15]. У даному випадку би будемо опиратись на процедуру реконструкції фазового простору, що згадувалась у лабораторних 2 і 3. Згідно пермутаційній процедурі ми будемо брати фрагмент ряду довжини $m$, що слугує розмірностю реконструйованого атрактора, та замінювати кожне значення ряду його порядковим індексом. На Рис. 4.1 представлено часовий ряд та його можливі порядкові шаблони:

Рис. 4.1: Фрагмент часового ряду (а) та 6 можливих порядкових шаблонів, що можуть зустрічатись у цьому сигналі (b)  [16]

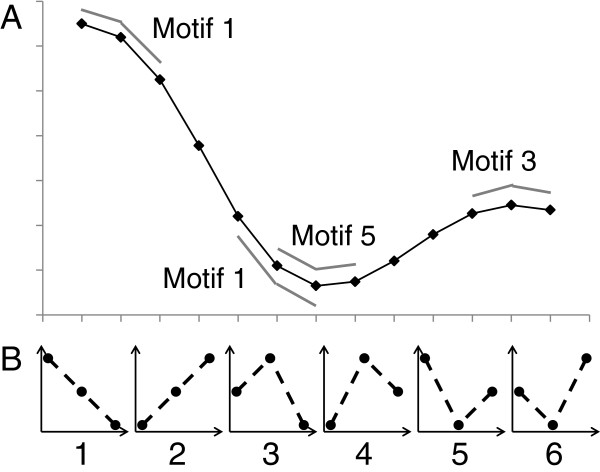
Алгоритм Лемпеля-Зіва виконує дві операції: (1) додає новий біт в уже існуючу послідовність; (2) копіює вже сформовану послідовність. Алгоритмічна складність представляє собою кількість таких операцій, необхідних для формування заданої послідовності.

Для випадкової послідовності довжини $n$ алгоритмічна складність обчислюється за виразом $LZ{C}_r=n/\log (n)$. Тоді відносна алгоритмічна складність знаходиться як відношення отриманої складності до складності випадкової послідовності: $LZC=LZC/LZ{C}_r$.

Однак навіть цього підходу може бути недостатньо. Справа в тому, що складні сигнали проявляють притаманну їм складність на різних просторових і часових масштабах, тобто мають масштабно інваріантні властивості. Вони, зокрема проявляються через степеневі закони розподілу. Тому мономасштабні розрахунки алгоритмічної складності можуть бути неприйнятними і призводити до помилкових висновків.

Для подолання таких труднощів використовуються мультимасштабні методи, до розгляду яких ми і переходимо.

4.1.3 Процедура грануляції для мультискейлінгового дослідження часових рядів. Мультимасштабні міри складності

Ідея цієї групи методів включає дві послідовно виконувані процедури:

1. процес “грубого дроблення” (coarse graining — “грануляції”) початкового часового ряду — усереднення даних на сегментах, що не перетинаються, розмір яких (вікно усереднення) збільшуватиметься на одиницю при переході на наступний за величиною масштаб;
2. обчислення на кожному з масштабів певного (до сих пір мономасштабного) показника складності.

Процес “грубого дроблення” (“грануляція”) полягає в усереднені послідовних відліків ряду в межах вікон, що не перетинаються, а розмір яких $\tau$ — збільшується при переході від масштабу до масштабу. Кожен елемент “гранульованого” часового ряду $y_j^{\tau }$ знаходиться у відповідності до виразу  [17]:

$$y_j^{\tau }=\frac{1}{\tau }\sum _{i=(j-1)\tau +1}^{j\tau }{x}_i,1\le j\le N/\tau ,$$

де $\tau$ характеризує фактор масштабування. Довжина кожного “гранульованого” ряду залежить від розміру вікна $і$ рівна $N/\tau$. Для масштабу рівного 1 “гранульований” ряд просто тотожний оригінальному.

Рис. 4.2: Схематична ілюстрація процесу грубого дроблення (“грануляції”) початкового часового ряду для масштабів 2 і 3

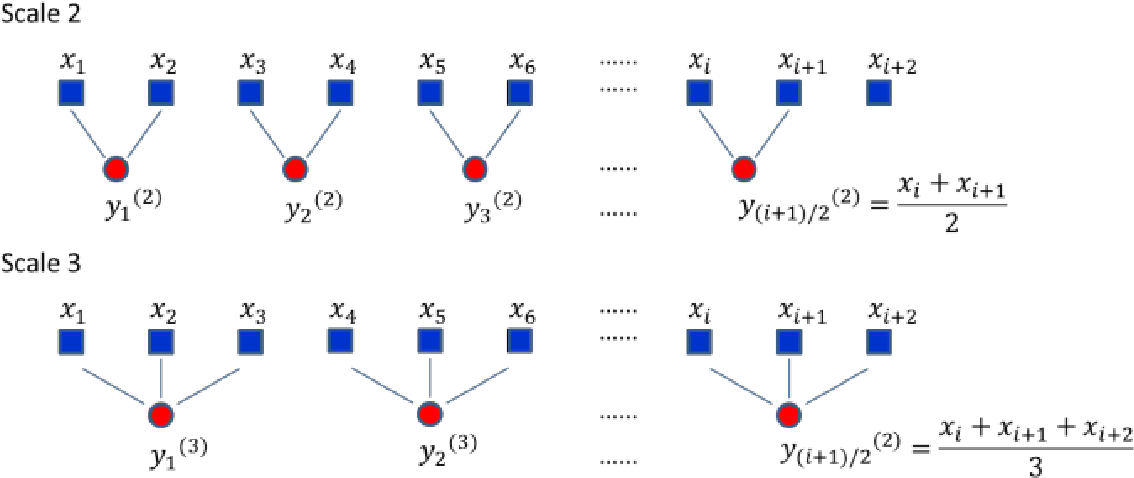
Бібліотека neurokit2 представляє метод для обчислення як мономасштабного показника складності Лемпеля-Зіва, так і його мультимасштабного аналогу.

Синтаксис мономасштабної процедури виглядає наступним чином:

complexity_lempelziv(signal, delay=1, dimension=2, permutation=False, symbolize='mean', **kwargs)

Параметри:

• signal (Union[list, np.array, pd.Series]) — сигнал;
• delay (int) — часова затримка, $\tau$. Використовується лише тоді, коли permutation=True;
• dimension (int) — розмірність вкладень, $m$. Використовується лише коли permutation=True;
• permutation (bool) — якщо значення True, поверне складність Лемпеля-Зіва на основі порядкових патернів;
• symbolize (str) — використовується тільки коли permutation=False. Метод перетворення неперервного сигналу на вході у символьний (дискретний) сигнал. За замовчуванням присвоює 0 та 1 значенням нижче та вище середнього. Може мати значення None, щоб пропустити процес (якщо вхідний сигнал вже є дискретним). Можна скористатися методом complexity_symbolize() для застосування іншої процедури символізації ряду;
• kwargs — інші аргументи, які передаються до complexity_ordinalpatterns() (якщо permutation=True) або complexity_symbolize().

Повертає:

• lzc (float) — складність Лемпеля-Зіва (LZC);
• info (dict) — словник, містить додаткову інформацію про параметри, що використовуються для обчислення LZC.

Синтаксис мультимасштабної процедури вже інший:

entropy_multiscale(signal, scale='default', dimension=3, tolerance='sd', method='MSEn', show=False, **kwargs)

Параметри:

• signal (Union[list, np.array, pd.Series]) — сигнал;
• scale (str або int або list) — список масштабних коефіцієнтів, що використовуються для процедури крос-грануляції часового ряду. Якщо значення "default", буде використано range(len(signal) / (dimension + 10)). Якщо "max", використовуватиме всі масштаби до половини довжини сигналу. Якщо ціле число, створить діапазон до вказаного цілого числа;
• dimension (int) — розмірність вкладення $m$;
• tolerance (float) — поріг пропускання $\epsilon$;
• method (str) — яку версію мультимасштабного показника обчислювати. Переважна кількість показників за цим методом відповідають ентропійним підходам. Нас цікавитиме саме "LZC";
• show (bool) — візуалізувати залежність показника від масштабу;
• kwargs — необов’язкові аргументи.

Повертає:

• float — точкова оцінка мультимасштабного показника окремого часового ряду, що відповідає площі під кривою значень цього показника, яка, по суті, є сумою вибіркових значень, наприклад, "LZC" в діапазоні масштабних коефіцієнтів;
• dict — словник, що містить додаткову інформацію щодо використаних для обчислення мультимасштабного показника параметрів. Значення показника, що відповідають кожному фактору "Scale", зберігаються під ключем "Value".

4.1.4 Шеннонівська складність

Ентропійний аналіз часових рядів за допомогою ентропійних показників різного роду буде проведено у наступних роботах. Зараз же ми розглянемо найпростішу з ентропій — ентропію Шеннона та порівняємо її можливості кількісно оцінювати складність часових послідовностей у порівнянні з мірою Лемпеля-Зіва.

Ентропія Шеннона (Shannon entropy) — це статистичний квантифікатор, який широко використовується для характеристики складних процесів. Поняття ентропії було використано Шенноном в теорії інформації для передачі даних  [6].

Ентропія - це міра невизначеності та випадковості системі. Якщо припустити, що всі наявні дані належать до одного класу, то неважко передбачити клас нових даних. Невизначеність, що виникає, коли подія $E$ відбувається з ймовірністю $p$, можна позначити як $S(p)$. Якщо ймовірність появи класу дорівнює 1, тоді ентропія мінімальна, $S(1)=0$. Відповідно до концепції Шеннона, якщо у нас наявні ймовірності реалізації певної події $p_1,p_2,p_3,...,p_n$, на виході отримується кількість інформації, що необхідна для опису цієї події. Тоді, Шеннонівська ентропія може бути визначена як

$$S=-\sum _{i=1}^n{p}_i\ln p_i.$$

Синтаксис методу для розрахунку Шеннонівської ентропії має вигляд:

entropy_shannon(signal=None, base=2, symbolize=None, show=False, freq=None, **kwargs)

Параметри:

• signal (Union[list, np.array, pd.Series]) — сигнал;
• base (float) — основа логарифму (за замовчуванням дорівнює 2). scipy.stats.entropy() за замовчуванням використовує число Ейлера (np.e) (натуральний логарифм), що дає міру інформації, виражену в натах;
• symbolize (str) — метод приведення неперервного сигналу на вході у символьний (дискретний) сигнал. За замовчуванням дорівнює нулю, що пропускає процес (вважається, що вхідні дані вже є дискретними);
• show (bool) — якщо значення True, виводить часовий ряд, де кожне значення розфарбоване у відповідності до класу до якого воно належить;
• freq (np.array) — замість сигналу можна надати вектор ймовірностей;
• kwargs — необов’язкові аргументи. Наразі не використовуються.

Повертає:

• shanen (float) — Шеннонівську ентропію;
• info (dict) — словник, що містить додаткову інформацію про параметри обчислення Шеннонівської ентропії.

4.1.5 Інформація Фішера

Інформацію Фішера (Fisher information, FI) було введено Р. А. Фішером у 1922 році як міру “внутрішньої точності” в теорії статистичних оцінок  [18]. Вона є центральною для багатьох статистичних застосувань, що виходять далеко за межі теорії складності. Даний показник вимірює кількість інформації, яку спостережувана випадкова величина несе про невідомий параметр. В аналізі складності вимірюється кількість інформації системи “про себе”. Він базується на розкладанні за сингулярними значеннями реконструйованого фазового простору. Величина FI зазвичай антикорельована з іншими показниками складності (чим більше інформації система приховує про себе, тим більш передбачуваною і, відповідно, менш складною вона є).

FI можна визначити, використовуючи метод fisher_information() бібліотеки neurokit2. Її синтаксис виглядає наступним чином:

fisher_information(signal, delay=1, dimension=2) з визначеними вже раніше параметрами

Повертає:

• fi (float) — обчислена міра FI;
• info (dict) — словник, що містить додаткову інформацію про параметри обчислення FI.

4.1.6 Складність Хьорта (Hjorth’s complexity) та його параметри

Параметри Хьорта — це показники статистичних властивостей, які спочатку були введені Хьортом  [19] для опису загальних характеристик сигналів електроенцифалограми. Параметрами є активність, рухливість і складність:

1. Параметр активності ($Activity$) — це просто дисперсія сигналу, яка відповідає середній потужності сигналу (якщо його середнє значення дорівнює 0):

$$Activity={\sigma }_{signal}^2.$$

2. Параметр рухливості ($Mobility$) являє собою середню частоту або частку середньоквадратичного відхилення спектра потужності. Він визначається як квадратний корінь з дисперсії першої похідної сигналу, поділений на дисперсію сигналу:

$$Mobility=\frac{{\sigma }_{dd}/{\sigma }_d}{Complexity}.$$

3. Параметр складності ($Complexity$) дає оцінку смуги пропускання сигналу, що вказує на схожість форми сигналу з чистою синусоїдою (для якої значення сходиться до 1). Іншими словами, це характеристика “надмірної деталізації” по відношенню до “найм’якшої” можливої форми кривої. Параметр “Складність” визначається як відношення рухливості першої похідної сигналу до рухливості самого сигналу:

$$Complexity={\sigma }_d/{\sigma }_{signal},$$

де $d$ та $dd$ представляють перші та другі похідні сигналу, відповідно.

Бібліотека neurokit2 представляє метод для отримання відповідних показників. Її синтаксис:

complexity_hjorth(signal)

Повертає:

• hjorth (float) — показник складності Хьорта;
• info (dict) — словник, що містить додаткові показники Хьорта "Mobility" та "Activity".

4.1.7 Час декореляції

Час декореляції (decorrelation time, DT) визначається як час (у відліках) першого перетину нуля функції автокореляції. Коротший DT відповідає менш корельованому сигналу. Наприклад, зменшення DT в сигналах електроенцифалограми спостерігається перед нападами, що пов’язано зі зменшенням потужності низьких частот  [20].

Бібліотека neurokit2 представляє функціонал для визначення DT, а саме метод complexity_decorrelation(). Її синтаксис:

complexity_decorrelation(signal)

Повертає:

• float — час декореляції;
• dict — словник, що містить додаткову інформацію про додаткові показники.

4.1.8 Відносна грубість (нерівність, шорсткість)

Відносна шорсткість (relative roughness, RLR) — це відношення локальної дисперсії (автоковаріації з лагом 1) до глобальної дисперсії (автоковаріації з лагом 0), яке можна використовувати для класифікації різних “шумів”. Цей показник також можна використовувати як індекс застосовності фрактального аналізу (показники фрактальності будуть описані в наступних роботах)  [21].

Синтаксис даного методу в бібліотеці neurokit2 виглядає наступним чином:

complexity_relativeroughness(signal, **kwargs)

Повертає:

• rr (float) — значення відносної грубості;
• info (dict) — словник, що містить інформацію відносно параметрів для обчислення показника грубості.

4.1.9 Взаємна інформація

Коли йдеться про виявлення зв’язків між змінними, ми часто використовуємо кореляцію Пірсона. Проблема полягає в тому, що цей показник знаходить лише лінійні зв’язки, що іноді може призвести до неправильної інтерпретації зв’язку між двома змінними. Інші статистичні методи вимірюють нелінійні зв’язки, такі як, наприклад, взаємна інформація (mutual information, MI)  [22].

MI між двома випадковими величинами вимірює нелінійний зв’язок між ними. Крім того, вона показує, яку кількість інформації можна отримати з випадкової величини, спостерігаючи за іншою випадковою величиною.

Вона тісно пов’язана з поняттям ентропії. Тобто, зменшення невизначеності випадкової величини корелює з отриманням інформації з іншої випадкової величини. І високе значення взаємної інформації вказує на помітне зменшення невизначеності. Якщо взаємна інформація дорівнює нулю, дві випадкові величини є незалежними.

MI можна розрахувати наступним чином:

$$I(X;Y)=\sum _{y\in Y}\sum _{x\in X}p(x,y)\cdot \log [p(x,y)/p(x)\cdot p(y)],$$

де $p(x)$ та $p(y)$ ймовірності спостереження окремо $x$ або $y$, а $p(x,y)$ ймовірність спостереження одночасно $x$ та $y$.

Основна відмінність між кореляцією та взаємною інформацією полягає в тому, що кореляція є мірою лінійної залежності, тоді як взаємна інформація вимірює загальну залежність (включаючи нелінійні зв’язки). Взаємна інформація дорівнює нулю, коли дві випадкові величини є строго незалежними.

Бібліотека neurokit2 представляє інструментарій для знаходження взаємної інформації між двома сигналами $x$ та $y$. У даній роботі ми спробуємо віднайти взаємну інформацію як між двома часовими рядами, так і авто-взаємну інформацію (auto-mutual information), подібно до автокореляції.

Синтаксис потрібної нам процедури:

mutual_information(x, y, method='varoquaux', bins='default', **kwargs)

Параметри:

• x і y (Union[list, np.array, pd.Series]) — масив значень;
• method (str) — метод для обчислення взаємної інформації: "nolitsa", "varoquaux", "knn", "max"’;
• bins (int) — кількість бінів гістограми. Використовується лише для "nolitsa" та "varoquaux". Якщо "default", кількість бінів оцінюється згідно методики описаної в  [23];
• kwargs — додаткові ключові аргументи для обраного методу.

Повертає:

• float — розрахована взаємна інформація.

Існують різноманітні підходи до розрахунку взаємної інформації:

• nolitsa: класична взаємна інформація;
• varoquaux: застосовує фільтр Гауса до об’єднаної гістограми. Величину згладжування можна налаштовувати за допомогою аргументу sigma (за замовчуванням sigma=1);
• knn: непараметрична (тобто не заснована на біннінгу) оцінка за найближчими сусідами. Додаткові параметри включають k (за замовчуванням, k=3), кількість найближчих сусідів для використання;
• max: максимальний коефіцієнт взаємної інформації, тобто $MI$ є максимальним при певній комбінації кількості бінів.

Розглянемо ефективність використання зазначених показників у якості індикаторів або індикаторів-передвісників крахових подій.

4.2 Хід роботи

Спочатку імпортуємо необхідні модулі для подальшої роботи:

import matplotlib.pyplot as plt 
import numpy as np
import neurokit2 as nk
import yfinance as yf
import pandas as pd
import scienceplots
from tqdm import tqdm

%matplotlib inline

І виконаємо налаштування рисунків для виведення:

plt.style.use(['science', 'notebook', 'grid']) # стиль, що використовуватиметься
                                               # для виведення рисунків

size = 16
params = {
    'figure.figsize': (8, 6),            # встановлюємо ширину та висоту рисунків за замовчуванням
    'font.size': size,                   # розмір фонтів рисунку
    'lines.linewidth': 2,                # товщина ліній
    'axes.titlesize': 'small',           # розмір титулки над рисунком
    'axes.labelsize': size,              # розмір підписів по осям
    'legend.fontsize': size,             # розмір легенди
    'xtick.labelsize': size,             # розмір розмітки по осі Ох
    'ytick.labelsize': size,             # розмір розмітки по осі Ох
    "font.family": "Serif",              # сімейство стилів підписів 
    "font.serif": ["Times New Roman"],   # стиль підпису
    'savefig.dpi': 300,                  # якість збережених зображень
    'axes.grid': False                   # побудова сітки на самому рисунку
}

plt.rcParams.update(params)              # оновлення стилю згідно налаштувань

Цього разу розглянему можливість побудови індикаторів-передвісників на прикладі фондового індексу S&P 500, але, окрім цього, додамо ще Біткоїн для розрахунку взаємної інформації між фондовим та криптовалютним ринками. Очевидно, що фондовий індекс S&P 500 має довшу ніж Біткоїн історію. До того ж, криптовалютний ринок працює безперервно на відміну від фондового. Тому треба буде об’єднати значення двох активів за тими датами, що співпадають.

Виконуємо зчитування фондового індексу:

symbol_1 = '^GSPC'         # Символ першого індексу
start_1 = "2014-01-01"     # Дата початку зчитування даних
end_1 = "2023-08-24"       # Дата закінчення зчитування даних

data_1 = yf.download(symbol_1, start_1, end_1)  # вивантажуємо дані
time_ser_1 = data_1['Close'].copy()         # зберігаємо саме ціни закриття

xlabel = 'time, days'      # підпис по вісі Ох 
ylabel_1 = symbol_1        # підпис по вісі Оу

YF.download() has changed argument auto_adjust default to True

[*********************100%***********************]  1 of 1 completed

Виконуємо зчитування криптовалютного індексу:

symbol_2 = 'BTC-USD'       # Символ другого індексу
start_2 = "2014-01-01"     # Дата початку зчитування даних
end_2 = "2023-08-24"       # Дата закінчення зчитування даних

data_2 = yf.download(symbol_2, start_2, end_2)  # вивантажуємо дані
time_ser_2 = data_2['Close'].copy()         # зберігаємо саме ціни закриття

xlabel = 'time, days'      # підпис по вісі Ох 
ylabel_2 = symbol_2        # підпис по вісі Оу

[*********************100%***********************]  1 of 1 completed

Увага

Виконайте цей блок, якщо хочете зчитати дані не з Yahoo! Finance, а із власного файлу. Зрозуміло, що й аналіз результатів, і висновки залежать від того, з яким рядом ми працюємо

---

symbol = 'sMpa11'                  # Символ індексу

path = "databases\sMpa11.txt"      # шлях по якому здійснюється зчитування файлу
data = pd.read_csv(path,           # зчитування даних 
                   names=[symbol])
time_ser = data[symbol].copy()     # копіюємо значення кривої 
                                   # "напруга-видовження" до окремої змінної

xlabel = r'$\varepsilon$'          # підпис по вісі Ох 
ylabel = symbol                    # підпис по вісі Оу

---

Тепер створимо новий масив даних, що об’єднуватиме в собі значення S&P 500 та BTC за їх спільними датами:

# приводимо значення індексів до типу DataFrame, щоб мати змогу їх об'єднати 
# за допомогою бібліотеки pandas
df_time_ser_1 = pd.DataFrame(time_ser_1) 
df_time_ser_2 = pd.DataFrame(time_ser_2)

joined = df_time_ser_1.merge(df_time_ser_2, # об'єднуємо по датам тієї бази, що містить 
                             on='Date',     # більше дат
                             how='left')  

joined = joined.rename(columns={joined.columns[0]: symbol_1,  # переіменовуємо колонки по 
                                joined.columns[1]: symbol_2}) # змінним symbol_1 та symbol_2

joined = joined.dropna()  # видаляємо рядки, що містять нульові значення

Виводимо отриману базу:

joined

Ticker	^GSPC	BTC-USD
Date
2014-09-17	2001.569946	457.334015
2014-09-18	2011.359985	424.440002
2014-09-19	2010.400024	394.795990
2014-09-22	1994.290039	402.152008
2014-09-23	1982.770020	435.790985
...	...	...
2023-08-17	4370.359863	26664.550781
2023-08-18	4369.709961	26049.556641
2023-08-21	4399.770020	26124.140625
2023-08-22	4387.549805	26031.656250
2023-08-23	4436.009766	26431.640625

2249 rows × 2 columns

І візуалізуємо сам графік. Спочатку оголосимо функцію для попарної візуалізації рядів зі збереженням їх абсолютних значень:

def plot_pair(x_values, y_values, x_label, y_label, file_name, clr="magenta"):

    fig, ax = plt.subplots()

    ax2 = ax.twinx()
    ax2.spines.right.set_position(("axes", 1.03))

    p1, = ax.plot(x_values, 
                  y_values[0], 
                  "b-", label=fr"{y_label[0]}")
    p2, = ax2.plot(x_values,
                   y_values[1], 
                   color=clr, 
                   label=fr'${y_label[1]}$')

    ax.set_xlabel(x_label)
    ax.set_ylabel(f"{y_label[0]}")

    ax.yaxis.label.set_color(p1.get_color())
    ax2.yaxis.label.set_color(p2.get_color())

    tkw = dict(size=2, width=1.5)

    ax.tick_params(axis='x', rotation=45, **tkw)
    ax.tick_params(axis='y', colors=p1.get_color(), **tkw)
    ax2.tick_params(axis='y', colors=p2.get_color(), **tkw)
    ax2.legend(handles=[p1, p2])

    plt.savefig(file_name + ".jpg")
        
    plt.show();

І тепер візуалізуємо отримані ряди:

values_plot = joined.iloc[:, 0].values, joined.iloc[:, 1].values
ylabels = ylabel_1, ylabel_2
file_name = f'joined {symbol_1}_{symbol_2}'

plot_pair(joined.index, values_plot, xlabel, ylabels, file_name)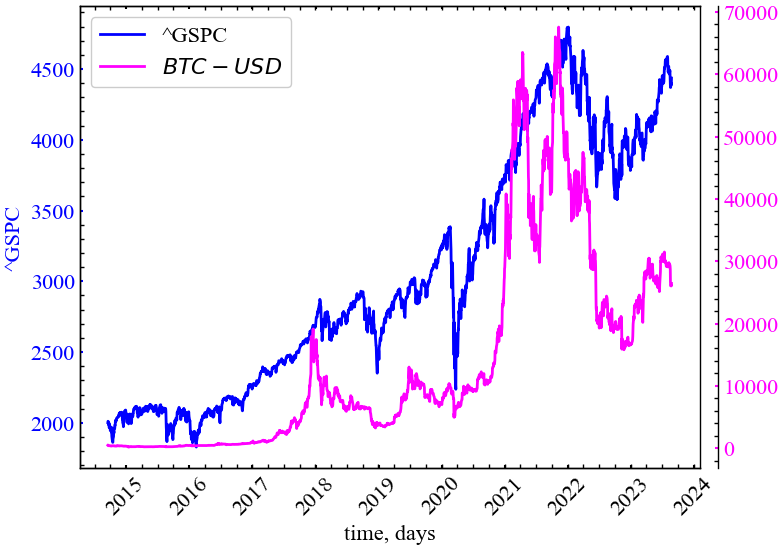

Рис. 4.3: Динаміка індексу S&P 500 та Біткоїна за досліджуваний період

Важливо

Не виконуйте блоки коду, що відповідають секції “Розрахунок взаємної інформації”, якщо ви працюєте з текстовим файлом

4.2.1 Розрахунок взаємної інформації

Розглянемо взаємну інформацію як індикатор нелінійної кореляції між двома фінансовими активами, і спробуємо визначити, чи є між ними “істинний” взаємозв’язок. Виконаємо розрахунки із використанням алгоритму руховому вікна. Також визначимо функцію transform() для нормалізації ряду:

def transformation(signal, ret_type):

    for_rec = signal.copy()

    if ret_type == 1:       # Зважаючи на вид ряду, виконуємо
                            # необхідні перетворення
        pass
    elif ret_type == 2:
        for_rec = for_rec.diff()
    elif ret_type == 3:
        for_rec = for_rec.pct_change()
    elif ret_type == 4:
        for_rec = for_rec.pct_change()
        for_rec -= for_rec.mean()
        for_rec /= for_rec.std()
    elif ret_type == 5: 
        for_rec = for_rec.pct_change()
        for_rec -= for_rec.mean()
        for_rec /= for_rec.std()
        for_rec = for_rec.abs()
    elif ret_type == 6:
        for_rec -= for_rec.mean()
        for_rec /= for_rec.std()

    for_rec = for_rec.dropna().values

    return for_rec

ret_type = 6                           # вид ряду
window = 100                           # ширина вікна
tstep = 1                              # часовий крок вікна 
length = len(joined.iloc[:,0].values)  # довжина самого ряду

MI = []                                # масив для віконної взаємної інформації

Тепер приступимо до розрахунків:

for i in tqdm(range(0,length-window,tstep)):       # фрагменти довжиною window  
                                                   # з кроком tstep

    # відбираємо фрагменти
    fragm_1 = joined[symbol_1][i:i+window]  
    fragm_2 = joined[symbol_2][i:i+window]

    # виконуємо процедуру трансформації ряду 
    fragm_1 = transformation(fragm_1, ret_type)    
    fragm_2 = transformation(fragm_2, ret_type)

    # розраховуємо взаємну інформацію 
    mut_inf = nk.mutual_information(fragm_1, fragm_2)
    
    # та додаємо результат до масиву значень
    MI.append(mut_inf)

100%|██████████| 2149/2149 [00:02<00:00, 869.31it/s]

Зберігаємо отриманий результат у текстовому файлі:

np.savetxt(f"mutual_inf_name1={symbol_1}_name2={symbol_2}_ \
    window={window}_step={tstep}_rettype={ret_type}.txt" , MI)

Візуалізуємо результат між відповідними показниками:

fig, ax = plt.subplots(1, 1)

ax2 = ax.twinx()
ax3 = ax.twinx()
ax2.spines.right.set_position(("axes", 1.03))
ax3.spines.right.set_position(("axes", 1.15))

p1, = ax.plot(joined.index[window:length:tstep], 
                joined[symbol_1][window:length:tstep].values, 
                "b-", 
                label=fr"{symbol_1}")
p2, = ax2.plot(joined.index[window:length:tstep],
                joined[symbol_2][window:length:tstep].values,
                'red', 
                label=fr"{symbol_2}")
p3, = ax3.plot(joined.index[window:length:tstep],
                MI,
                'magenta', 
                label=r"$MI$")               

ax.set_xlabel(xlabel)
ax.set_ylabel(f"{symbol_1}")
ax.yaxis.label.set_color(p1.get_color())
ax2.yaxis.label.set_color(p2.get_color())
ax3.yaxis.label.set_color(p3.get_color())

tkw = dict(size=3, width=1.5)

ax.tick_params(axis='x', rotation=45, **tkw)
ax.tick_params(axis='y', colors=p1.get_color(), **tkw)
ax2.tick_params(axis='y', colors=p2.get_color(), **tkw)
ax3.tick_params(axis='y', colors=p3.get_color(), **tkw)
ax3.legend(handles=[p1, p2, p3])

plt.savefig(f"mutual_inf_name1={symbol_1}_name2={symbol_2}_ \
    window={window}_step={tstep}_rettype={ret_type}.jpg")

plt.show();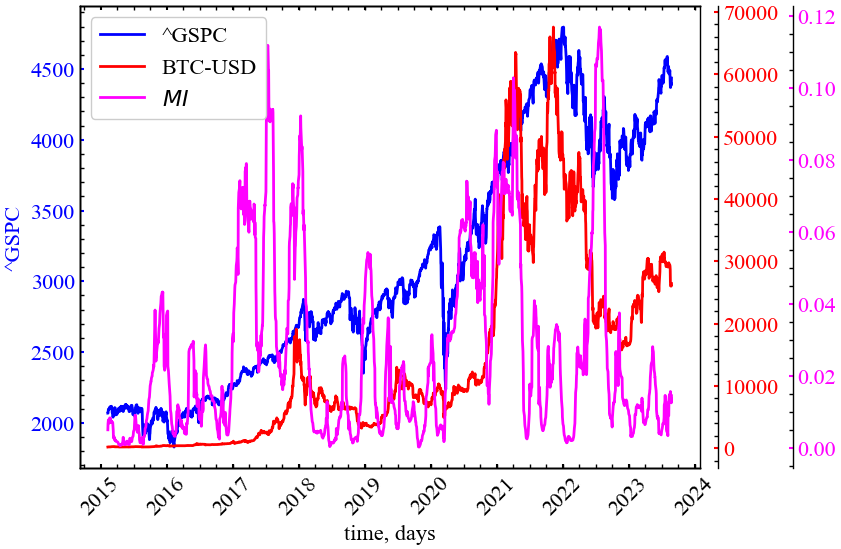

Рис. 4.4: Динаміка індексу S&P 500, Біткоїна та взаємної інформації

Як ми можемо бачити з представленого рисунку, як на фондовому так і криптовалютному ринках дійсно спостерігалися фази зростання взаємної інформації. Найкраще це видно напередодні кризи 2018-го року, під час 2019 року, після коронавірусної пандемії та напередодні 2023 року. Для даного індикатора залишається простір для експериментів, що можуть вивести його на рівень достатньо потужного передвісника криз на фінансових ринках.

Як вже зазначалося, окрім обчислення взаємної інформації для двох пар часових сигналів, ми можемо обчислити автовзаємну інформацію.

Для цього визначимо наступну функцію:

def automut(x, maxlag):
    n = len(x)                               # визначаємо довжину сигналу
    lags = np.arange(0, maxlag, dtype="int") # оголошуємо масив лагів від 0 до maxlag
    mi = np.zeros(len(lags))                 # оголошуємо масив під значення взаємної інформації
    for i, lag in enumerate(lags):           # проходимось по кожному лагу
        
        # виконуємо зміщення на lag значень 
        y1 = x[:n-lag].copy()
        y2 = x[lag:].copy()

        # і розраховуємо взаємну інформацію між часовим рядом y1
        # та його зміщенною на lag кроків копією 
        mi[i] = nk.mutual_information(y1, y2, bins=100)

    return mi

Виведемо залежність автовзаємної інформації від лагу для всього ряду S&P 500 та Біткоїна. Спочатку розрахуємо вихідні значення ряду, далі прибутковості і потім волатильності. Для кожного з відповідних сигналів виведемо взаємну інформацію.

Виконуємо перетворення S&P 500 та Біткоїна:

sp_init = transformation(time_ser_1, ret_type=1).flatten()
sp_ret = transformation(time_ser_1, ret_type=4).flatten()
sp_vol = np.abs(sp_ret.copy())

btc_init = transformation(time_ser_2, ret_type=1).flatten()
btc_ret = transformation(time_ser_2, ret_type=4).flatten()
btc_vol = np.abs(btc_ret.copy())

Розраховуємо автовзаємну інформацію S&P 500 та Біткоїна:

max_lag = 100

mu_sp_init = automut(sp_init, max_lag)
mu_sp_ret = automut(sp_ret, max_lag)
mu_sp_vol = automut(sp_vol, max_lag)

mu_btc_init = automut(btc_init, max_lag)
mu_btc_ret = automut(btc_ret, max_lag)
mu_btc_vol = automut(btc_vol, max_lag)

lags = np.arange(0, max_lag, dtype="int") # оголошуємо масив лагів від 0 до maxlag

fig, ax = plt.subplots(1, 1)                # Створюємо порожній графік

ax.plot(lags, mu_sp_init, label=r'$MI $ ' + f'{symbol_1}')  # Додаємо дані до графіку
ax.plot(lags, mu_sp_ret, label=r'$MI$ ' + r'$g(t)$')                          
ax.plot(lags, mu_sp_vol, label=r'$MI$ ' +  r'$V_{T}$') 

ax.legend()                                 # Додаємо легенду
ax.set_xlabel("Часова затримка")            # Додаємо підпис для вісі Ох
ax.set_ylabel("Авто-взаємна інформація")    # Додаємо підпис для вісі Оу

plt.savefig(f'Automutual information {symbol_1}.jpg')  # Зберігаємо графік 
plt.show();                                            # Виводимо графік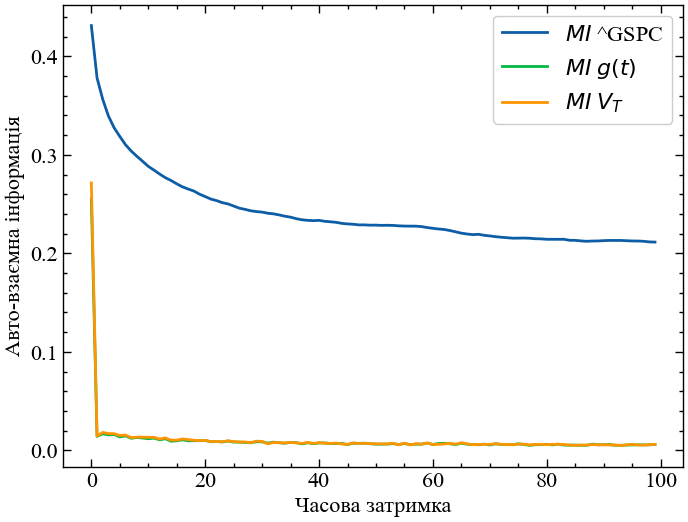

Рис. 4.5: Зміна з часом автовзаємної інформації для вихідного ряду x, нормалізованих прибутковостей g та модулів mod(g) фондового індексу S&P 500

fig, ax = plt.subplots()                     # Створюємо порожній графік

ax.plot(lags, mu_btc_init, label=r'$MI $ ' + f'{symbol_2}')  # Додаємо дані до графіку
ax.plot(lags, mu_btc_ret, label=r'$MI$ ' + r'$g(t)$')                          
ax.plot(lags, mu_btc_vol, label=r'$MI$ ' +  r'$V_{T}$') 

ax.legend()                                 # Додаємо легенду
ax.set_xlabel("Часова затримка")            # Додаємо підпис для вісі Ох
ax.set_ylabel("Авто-взаємна інформація")    # Додаємо підпис для вісі Оу

plt.savefig(f'Automutual information {symbol_2}.jpg')  # Зберігаємо графік 
plt.show();                                            # Виводимо графік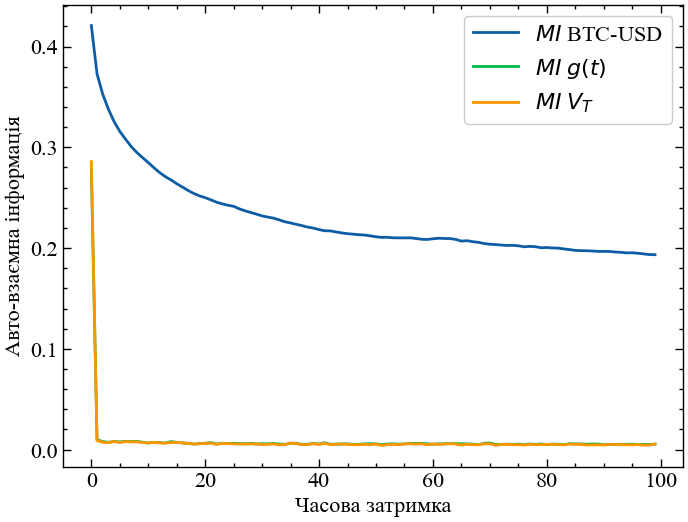

Рис. 4.6: Зміна з часом автовзаємної інформації для вихідного ряду x, нормалізованих прибутковостей g та модулів mod(g) криптовалютного індексу BTC

Очевидно, ступінь взаємної інформації це показник, що найкращим чином працює саме для вихідних значень часових сигналів. Для вихідного ряду ступінь взаємної інформації залишається доволі високим. Для прибутковостей і волатильностей взаємна інформація спадає одразу на першому лагу, що свідчить про незалежність значень на подальших часових затримках.

4.2.2 Розрахунок мономасштабної складності Лемпеля-Зіва

Продовжимо розраховувати й інші показники складності. Розглянемо можливість використання показника складності Лемпеля-Зіва в якості індикатора катастрофічних подій:

ret_type = 4                           # вид ряду
window = 250                           # ширина вікна
tstep = 1                              # часовий крок вікна 
length = len(time_ser_1.values)        # довжина самого ряду
m = 4                                  # розмірність вкладень 
tau = 1                                # часова затримка         

LZC = []                               # класична складність Лемпеля-Зіва
PLZC = []                              # пермутаційна складність Лемпеля-Зіва

for i in tqdm(range(0,length-window,tstep)):    # фрагменти довжиною window  
                                                # з кроком tstep

    # відбираємо фрагмент
    fragm = time_ser_1.iloc[i:i+window].copy()   

    # виконуємо процедуру трансформації ряду 
    fragm = transformation(fragm, ret_type).flatten()

    # розраховуємо класичну складність Лемпеля-Зіва 
    lzc, _ = nk.complexity_lempelziv(fragm)

    # та пермутаційну складність Лемпеля-Зіва
    plzc, _ = nk.complexity_lempelziv(fragm, 
                                      delay=tau, 
                                      dimension=m, 
                                      permutation=True)

    # та додаємо результати до масиву значень
    LZC.append(lzc)
    PLZC.append(plzc)

100%|██████████| 2177/2177 [00:14<00:00, 153.81it/s]

Зберігаємо результати в текстових файлах:

np.savetxt(f"lzc_name={symbol_1}_window={window}_step={tstep}_rettype={ret_type}.txt" , LZC)
np.savetxt(f"plzc_name={symbol_1}_window={window}_step={tstep}_ \
    rettype={ret_type}_m={m}_tau={tau}.txt" , PLZC)

Та візуалізуємо їх:

fig, ax = plt.subplots(1, 1)

ax2 = ax.twinx()
ax3 = ax.twinx()
ax2.spines.right.set_position(("axes", 1.03))
ax3.spines.right.set_position(("axes", 1.12))

p1, = ax.plot(time_ser_1.index[window:length:tstep], 
                time_ser_1.values[window:length:tstep], 
                "b-", 
                label=fr"{symbol_1}")
p2, = ax2.plot(time_ser_1.index[window:length:tstep],
                LZC,
                'gold', 
                label=fr"$LZC$")
p3, = ax3.plot(time_ser_1.index[window:length:tstep],
                PLZC,
                'red', 
                label=fr"$PLZC$")               


ax.set_xlabel(xlabel)
ax.set_ylabel(f"{symbol_1}")
ax.yaxis.label.set_color(p1.get_color())
ax2.yaxis.label.set_color(p2.get_color())
ax3.yaxis.label.set_color(p3.get_color())

tkw = dict(size=3, width=1.5)

ax.tick_params(axis='x', rotation=45, **tkw)
ax.tick_params(axis='y', colors=p1.get_color(), **tkw)
ax2.tick_params(axis='y', colors=p2.get_color(), **tkw)
ax3.tick_params(axis='y', colors=p3.get_color(), **tkw)
ax3.legend(handles=[p1, p2, p3])

plt.savefig(f"plzc_lzc_name={symbol_1}_ \
    window={window}_step={tstep}_ \
    rettype={ret_type}_m={m}_tau={tau}.jpg")

plt.show();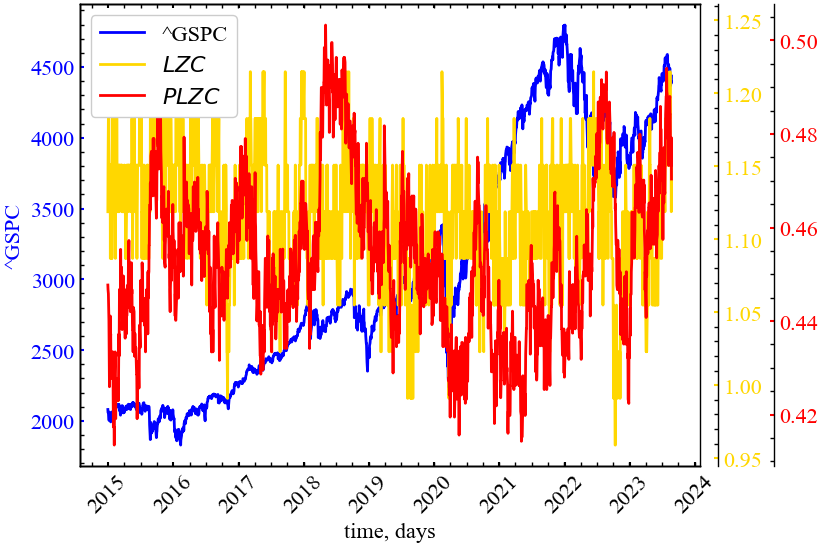

Рис. 4.7: Динаміка індексу S&P 500, класичної мономасштабної складності Лемпеля-Зіва та її пермутаційного аналогу

На даному рисунку видно, що 2 міри поводять себе асиметрично по відношенню один до одного: $LCZ$ вказує на зростання складності, наприклад, події 2019 року. У той же час $PLCZ$ вказує на спад складності системи в цей період. Варто дослідити мультимасштабну динаміку міри Лемпеля-Зіва для більш змістовних висновків.

4.2.3 Обчислення мультимасштабної складності Лемпеля-Зіва

Розрахуємо віконну динаміку мультимасштабних показників Лемпеля-Зіва. Ми повертаємо сумарну складність Лемпеля-Зіва за всіма масштабами:

ret_type = 4                      # вид ряду
window = 250                      # ширина вікна
tstep = 1                         # часовий крок вікна 
length = len(time_ser_1.values)   # довжина самого ряду
m = 4                             # розмірність вкладень 
tau = 1                           # часова затримка         

MSLZC = []                        # мультимасштабна складність Лемпеля-Зіва
MSPLZC = []                       # мультимасштабна пермутаційна складність Лемпеля-Зіва

for i in tqdm(range(0,length-window,tstep)):    # фрагменти довжиною window  
                                                # з кроком tstep

    # відбираємо фрагмент
    fragm = time_ser_1.iloc[i:i+window].copy()   

    # виконуємо процедуру трансформації ряду 
    fragm = transformation(fragm, ret_type).flatten()

    # розраховуємо мультимасштабну складність Лемпеля-Зіва 
    mslzc, _ = nk.entropy_multiscale(fragm)

    # та мультимасштабну пермутаційну складність Лемпеля-Зіва
    msplzc, _ = nk.entropy_multiscale(fragm, 
                                      delay=tau, 
                                      dimension=m, 
                                      permutation=True)


    # та додаємо результати до масиву значень
    MSLZC.append(mslzc)
    MSPLZC.append(msplzc)

100%|██████████| 2177/2177 [00:59<00:00, 36.76it/s]

np.savetxt(f"mslzc_name={symbol_1}_window={window}_step={tstep}_ \
    rettype={ret_type}.txt" , MSLZC)
np.savetxt(f"msplzc_name={symbol_1}_window={window}_step={tstep}_ \
    rettype={ret_type}_m={m}_tau={tau}.txt" , MSPLZC)

fig, ax = plt.subplots(1, 1)

ax2 = ax.twinx()
ax3 = ax.twinx()
ax2.spines.right.set_position(("axes", 1.03))
ax3.spines.right.set_position(("axes", 1.12))

p1, = ax.plot(time_ser_1.index[window:length:tstep], 
                time_ser_1.values[window:length:tstep], 
                "b-", 
                label=fr"{symbol_1}")
p2, = ax2.plot(time_ser_1.index[window:length:tstep],
                MSLZC,
                'gold', 
                label=fr"$MSLZC$")
p3, = ax3.plot(time_ser_1.index[window:length:tstep],
                MSPLZC,
                'red', 
                label=fr"$MSPLZC$")               

ax.set_xlabel(xlabel)
ax.set_ylabel(f"{symbol_1}")
ax.yaxis.label.set_color(p1.get_color())
ax2.yaxis.label.set_color(p2.get_color())
ax3.yaxis.label.set_color(p3.get_color())

tkw = dict(size=3, width=1.5)

ax.tick_params(axis='x', rotation=45, **tkw)
ax.tick_params(axis='y', colors=p1.get_color(), **tkw)
ax2.tick_params(axis='y', colors=p2.get_color(), **tkw)
ax3.tick_params(axis='y', colors=p3.get_color(), **tkw)
ax3.legend(handles=[p1, p2, p3])

plt.savefig(f"msplzc_mslzc_name={symbol_1}_ \
    window={window}_step={tstep}_ \
    rettype={ret_type}_m={m}_tau={tau}.jpg")

plt.show();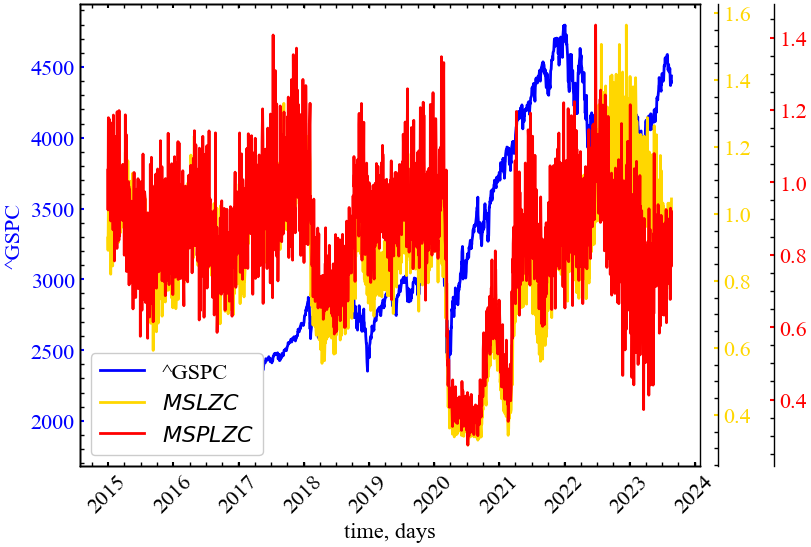

Рис. 4.8: Динаміка індексу S&P 500, класичної мультимасштабної складності Лемпеля-Зіва та її пермутаційного аналогу

Тепер бачимо однозначну картину: обидві міри поводять себе синхронно, та спадають у кризові та передкризові періоди, що вказує на зростання ступеня детермінованості та самоорганізації ринку.

4.2.4 Обчислення Шеннонівської ентропії

Як уже зазначалося, Шеннонівська ентропія — це міра непередбачуваності стану, або, еквівалентно, його середнього інформаційного вмісту. Ентропія Шеннона є однією з перших і найбільш базових мір ентропії та фундаментальним поняттям теорії інформації.

Розраховуватимемо її в ковзному вікні:

ret_type = 1                      # вид ряду
window = 250                      # ширина вікна
tstep = 1                         # часовий крок вікна 
length = len(time_ser_1.values)   # довжина самого ряду  
log_base = np.exp(1)      

shannon = []                      # ентропія Шеннона

for i in tqdm(range(0,length-window,tstep)):       # фрагменти довжиною window  
                                                   # з кроком tstep

    # відбираємо фрагмент
    fragm = time_ser_1.iloc[i:i+window].copy()   

    # виконуємо процедуру трансформації ряду 
    fragm = transformation(fragm, ret_type)

    # розраховуємо ентропію Шеннона
    p, be = np.histogram(fragm,         # розраховуємо щільність ймовірностей
                        bins='auto', 
                        density=True)  
    r = be[1:] - be[:-1]                # знаходимо dx
    P = p * r                           # представляємо ймовірність як f(x)*dx
    P = P[P!=0]                         # фільтруємо по всім ненульовим ймовірностям

    sh_ent, _ = nk.entropy_shannon(freq=P, base=log_base) # розраховуємо ентропію 
    sh_ent /= np.log(len(P))                              # та нормалізуємо

    # та додаємо результат до масиву значень
    shannon.append(sh_ent)

100%|██████████| 2177/2177 [00:01<00:00, 1211.19it/s]

np.savetxt(f"shannon_ent_name={symbol_1}_window={window}_ \
    step={tstep}_rettype={ret_type}.txt" , shannon)

values_plot = time_ser_1.values[window:length:tstep], shannon
ylabels = ylabel_1, "ShEn"
file_name = f"shannon_ent_name={symbol_1}_window={window}_ \
    step={tstep}_rettype={ret_type}"

plot_pair(time_ser_1.index[window:length:tstep], 
            values_plot, xlabel, ylabels, file_name)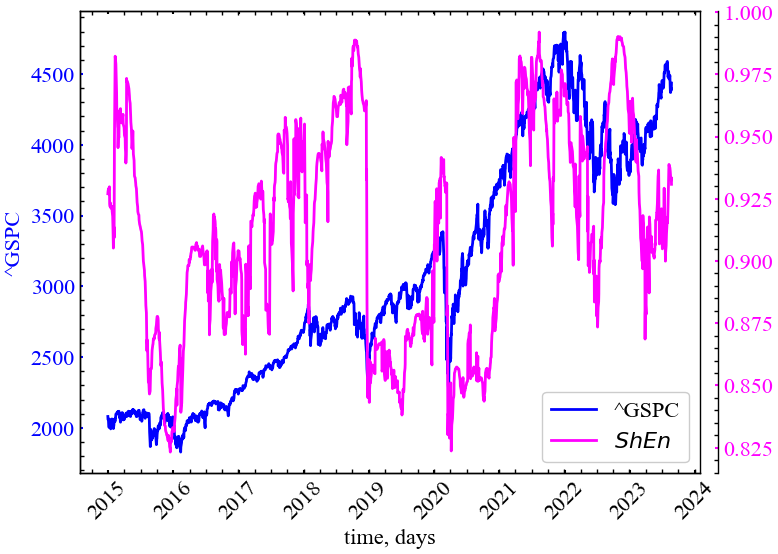

Рис. 4.9: Динаміка індексу S&P 500 та ентропії Шеннона

Як ми можемо бачити з представленого рисунку, ентропія Шеннона реагує спадом на кризові періоди індексу S&P 500, що вказує на приріст ступеня кореляції системи, її детермінованості.

4.2.5 Розрахунок інформаційного показника Фішера

Перш за все задаємо параметри для розрахунків:

ret_type = 1                      # вид ряду
window = 250                      # ширина вікна
tstep = 1                         # часовий крок вікна 
length = len(time_ser_1.values)   # довжина самого ряду  
m = 3                             # розмірність вкладень
tau = 1                           # часова затримка

fisher = []                       # інформація Фішера

for i in tqdm(range(0,length-window,tstep)):       # фрагменти довжиною window  
                                                   # з кроком tstep

    # відбираємо фрагмент
    fragm = time_ser_1.iloc[i:i+window].copy()   

    # виконуємо процедуру трансформації ряду 
    fragm = transformation(fragm, ret_type).flatten()

    fish_inf, _ = nk.fisher_information(signal=fragm,
                                        dimension=m, 
                                        delay=tau) 

    # та додаємо результат до масиву значень
    fisher.append(fish_inf)

100%|██████████| 2177/2177 [00:01<00:00, 1909.22it/s]

np.savetxt(f"fisher_inf_name={symbol_1}_window={window}_ \
    step={tstep}_rettype={ret_type}_dimension={m}_delay={tau}.txt", fisher)

values_plot = time_ser_1.values[window:length:tstep], fisher
ylabels = ylabel_1, "FI"
file_name = f"fisher_name={symbol_1}_window={window}_ \
    step={tstep}_rettype={ret_type}_dimension={m}_delay={tau}"

plot_pair(time_ser_1.index[window:length:tstep], values_plot, xlabel, ylabels, file_name)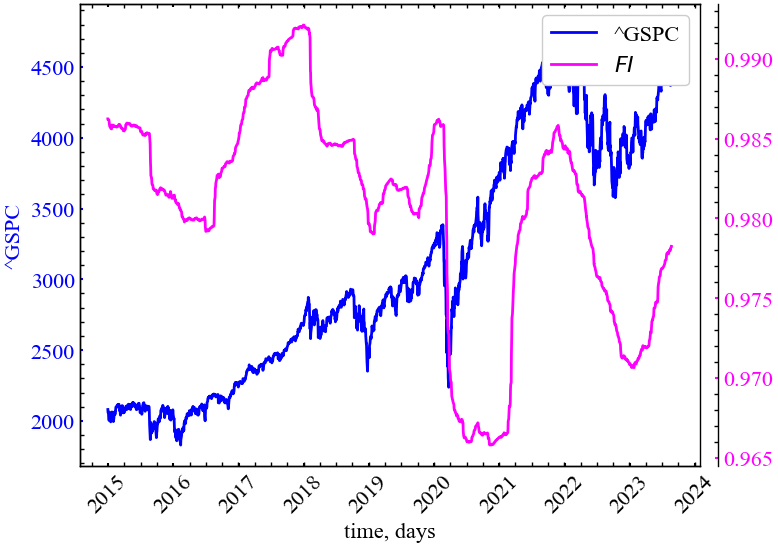

Рис. 4.10: Динаміка індексу S&P 500 та інформаційного показника Фішера

З Рис. 4.10 видно, що показник Фішера спадає у кризові та передкризові періоди, що говорить про спад кількості необхідної для опису самоорганізованої динаміки фінансових криз інформації, зростання корельованості між діями трейдерів на ринку.

4.2.6 Обчислення часу декореляції

ret_type = 1                      # вид ряду
window = 250                      # ширина вікна
tstep = 1                         # часовий крок вікна 
length = len(time_ser_1.values)   # довжина самого ряду 

decorrelation_time = []           # час декореляції

for i in tqdm(range(0,length-window,tstep)):       # фрагменти довжиною window  
                                                   # з кроком tstep

    # відбираємо фрагмент
    fragm = time_ser_1.iloc[i:i+window].copy()   

    # виконуємо процедуру трансформації ряду 
    fragm = transformation(fragm, ret_type).flatten()

    dec_time, _ = nk.complexity_decorrelation(fragm) 

    # та додаємо результат до масиву значень
    decorrelation_time.append(dec_time)

100%|██████████| 2177/2177 [00:01<00:00, 1390.17it/s]

np.savetxt(f"dec_time_name={symbol_1}_window={window}_ \
    step={tstep}_rettype={ret_type}.txt", decorrelation_time)

values_plot = time_ser_1.values[window:length:tstep], decorrelation_time
ylabels = ylabel_1, "DT"
file_name = f"dec_time_name={symbol_1}_window={window}_ \
    step={tstep}_rettype={ret_type}"

plot_pair(time_ser_1.index[window:length:tstep], values_plot, 
            xlabel, ylabels, file_name)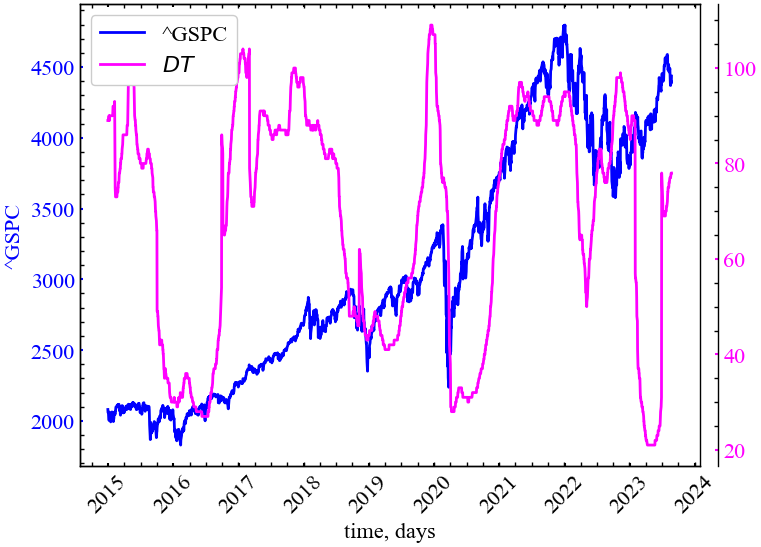

Рис. 4.11: Динаміка індексу S&P 500 та часу декореляції

Час декореляції зростає у передкраховий період, що вказує на посилення кореляції системи в цей період.

4.2.7 Обчислення відносної шорсткості

ret_type = 1                      # вид ряду
window = 250                      # ширина вікна
tstep = 1                         # часовий крок вікна 
length = len(time_ser_1.values)   # довжина самого ряду 

relative_roughness = []           # відносна шорсткість

for i in tqdm(range(0,length-window,tstep)): # фрагменти довжиною window  
                                             # з кроком tstep

    # відбираємо фрагмент
    fragm = time_ser_1.iloc[i:i+window].copy()   

    # виконуємо процедуру трансформації ряду 
    fragm = transformation(fragm, ret_type).flatten()

    rr, _ = nk.complexity_relativeroughness(fragm) 

    # та додаємо результат до масиву значень
    relative_roughness.append(rr)

100%|██████████| 2177/2177 [00:01<00:00, 1286.27it/s]

np.savetxt(f"rel_rough_name={symbol_1}_window={window}_ \
    step={tstep}_rettype={ret_type}.txt", relative_roughness)

values_plot = time_ser_1.values[window:length:tstep], relative_roughness
ylabels = ylabel_1, "RR"
file_name = f"rel_rough={symbol_1}_window={window}_ \
    step={tstep}_rettype={ret_type}"

plot_pair(time_ser_1.index[window:length:tstep], values_plot, 
            xlabel, ylabels, file_name)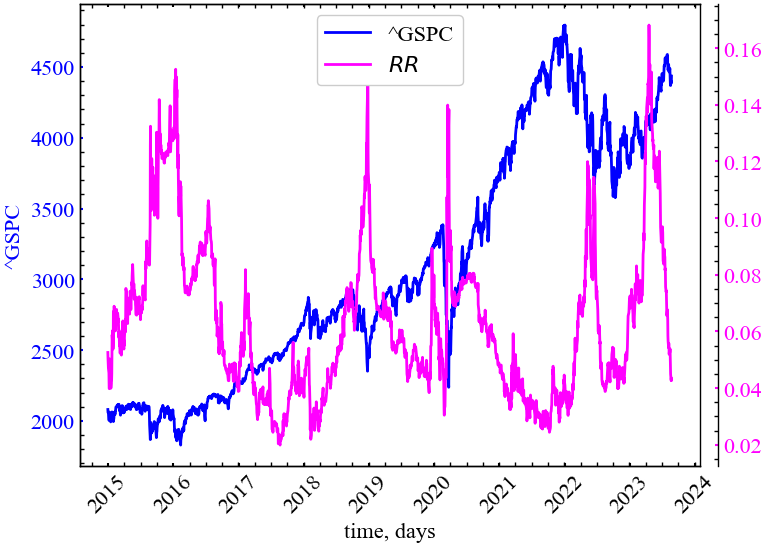

Рис. 4.12: Динаміка індексу S&P 500 та показника відносної шорсткості

Показник відносної шорсткості демонструє, що крахові події як, наприклад, у 2015, 2016, 2019, 2020 та 2023 роках характеризуються зростанням шорсткості. Подібного роду поведінка є індикатором зростання шумової активності ринку: кореляційних характеристик та загальної варіації ринку в цілому.

4.2.8 Розрахунок показників складності Хьорта

Завершуємо хід роботи показниками складності Хьорта:

ret_type = 1                      # вид ряду
window = 250                      # ширина вікна
tstep = 1                         # часовий крок вікна 
length = len(time_ser_1.values)   # довжина самого ряду 

activity = []                     # параметр активності
mobility = []                     # параметр рухливості
complexity = []                   # параметр складності

for i in tqdm(range(0,length-window,tstep)): # фрагменти довжиною window  
                                             # з кроком tstep

    # відбираємо фрагмент
    fragm = time_ser_1.iloc[i:i+window].copy()   

    # виконуємо процедуру трансформації ряду 
    fragm = transformation(fragm, ret_type).flatten()

    # розраховуємо показники складності Хьорта
    cmpl, info = nk.complexity_hjorth(fragm) 

    # та додаємо результат до масиву значень
    activity.append(info['Activity'])
    mobility.append(info['Mobility'])
    complexity.append(cmpl)

100%|██████████| 2177/2177 [00:01<00:00, 1756.67it/s]

np.savetxt(f"activity_name={symbol_1}_window={window}_ \
    step={tstep}_rettype={ret_type}.txt", activity)
np.savetxt(f"mobility_name={symbol_1}_window={window}_ \
    step={tstep}_rettype={ret_type}.txt", mobility)
np.savetxt(f"complexity_name={symbol_1}_window={window}_ \
    step={tstep}_rettype={ret_type}.txt", complexity)    

fig, ax = plt.subplots(1, 1)

ax2 = ax.twinx()
ax3 = ax.twinx()
ax4 = ax.twinx()

ax2.spines.right.set_position(("axes", 1.03))
ax3.spines.right.set_position(("axes", 1.16))
ax4.spines.right.set_position(("axes", 1.24))

p1, = ax.plot(time_ser_1.index[window:length:tstep], 
              time_ser_1.values[window:length:tstep], 
              "b-", label=fr"{ylabel_1}")
p2, = ax2.plot(time_ser_1.index[window:length:tstep], 
               activity, "r--", label=r"$Act$")
p3, = ax3.plot(time_ser_1.index[window:length:tstep], 
               mobility, "g-", label=r"$Mob$")
p4, = ax4.plot(time_ser_1.index[window:length:tstep],
               complexity, "m-", label=r"$Comp$")

ax.set_xlabel(xlabel)
ax.set_ylabel(f"{ylabel_1}")
ax.yaxis.label.set_color(p1.get_color())
ax2.yaxis.label.set_color(p2.get_color())
ax3.yaxis.label.set_color(p3.get_color())
ax4.yaxis.label.set_color(p4.get_color())

tkw = dict(size=4, width=1.5)

ax.tick_params(axis='y', colors=p1.get_color(), **tkw)
ax.tick_params(axis='x', rotation=45, **tkw)
ax2.tick_params(axis='y', colors=p2.get_color(), **tkw)
ax3.tick_params(axis='y', colors=p3.get_color(), **tkw)
ax4.tick_params(axis='y', colors=p4.get_color(), **tkw)
ax4.legend(handles=[p1, p2, p3, p4])

plt.savefig(f"hjorth_name={symbol_1}_ret={ret_type}_wind={window}_step={tstep}.jpg")
plt.show();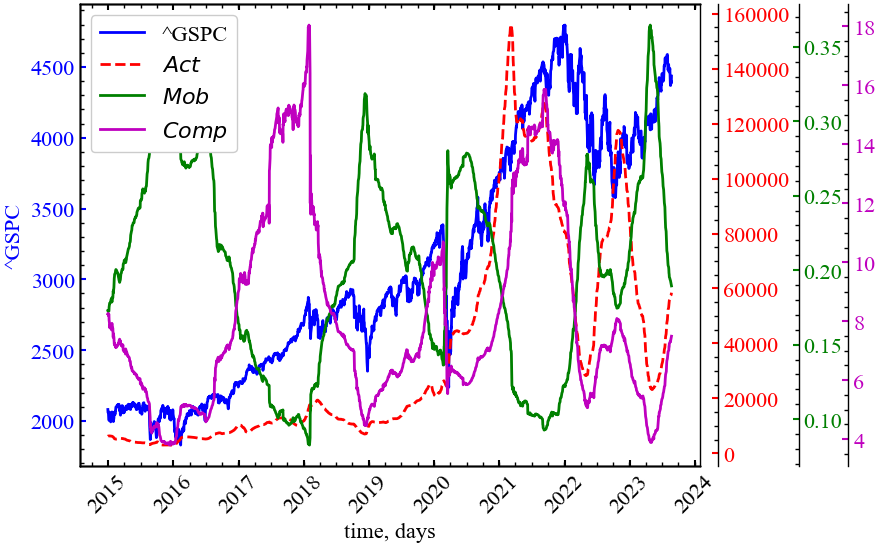

Рис. 4.13: Динаміка індексу S&P500 наряду з показниками активності, мобільності та складності Хьорта

Очевидно, що параметр активності ($Act$) представляється найменш інформативним, оскільки він вказує тільки на зростання сукупної дисперсії сигналу. Активність почала помітно зростати напередодні 2022 року, але для попередніх кризових станів ми не бачимо передвісницької поведінки цього індикатора. Питання передчасної ідентифікації наростання кризового явища найкраще вирішує показник мобільності ($Mob$). Ми бачимо, що даний показник зростає під час 2015-2016 років, напередодні 2019 року, при настанні коронавірусної пандемії, перед 2023 та 2024 роками. Показник складності Хьорта ($Comp$) реагує асиметричним чином: у той час коли мобільність зростає, показник складності спадає, вказуючи на те, що система прагне до вищого ступеня періодичності або корельованості.

4.3 Висновок

Таким чином, розглянуті інформаційні міри складності дозволяють дослідити певні аспекти складності систем будь-якої природи. Особливо продуктивним являється мультимасштабна версія введених мір. Ретельний аналіз часових рядів для систем різної природи, різного рівня складності, порівняння їх із тестовими сигналами, вивчення поведінки систем у різних (не обов’язково рівноважних, стаціонарних) умовах дозволить зрозуміти природу складності і спрогнозувати можливу поведінку систем у критичних умовах. Так, порівняння вихідного часового ряду з відповідними мірами складності свідчить про очевидне їх реагування на кризові явища. Однак питання використання їх у якості передвісників вимагає додаткових досліджень.

4.4 Завдання для самостійної роботи

1. Дослідіть і порівняйте результати для фінансових рядів, що представляють розвинені компанії (країни, криптовалюти) і такі, що розвиваються. Порівняйте результати. Поясніть, в чому їх схожість та відмінності
2. Яким чином поводять себе міри складності у період фінансових шоків і криз?
3. Наскільки чутливими є результати розрахунків до вибору ширини вікна та кроку?

[1]

M. S. Kanwal, J. A. Grochow, and N. Ay, Comparing information-theoretic measures of complexity in boltzmann machines, Entropy 19, (2017).

[2]

A. N. Kolmogorov, Three approaches to the quantitative definition of information, International Journal of Computer Mathematics 2, 157 (1968).

[3]

D. G. Bonchev, Information Theoretic Complexity Measures, in Encyclopedia of Complexity and Systems Science, edited by R. A. Meyers (Springer New York, New York, NY, 2009), pp. 4820–4839.

[4]

L. T. Lui, G. Terrazas, H. Zenil, C. Alexander, and N. Krasnogor, Complexity Measurement Based on Information Theory and Kolmogorov Complexity, Artificial Life 21, 205 (2015).

[5]

M. Li and P. Vitányi, Preliminaries, in An Introduction to Kolmogorov Complexity and Its Applications (Springer New York, New York, NY, 2008), pp. 1–99.

[6]

C. E. Shannon, A mathematical theory of communication, Bell System Technical Journal 27, 379 (1948).

[7]

A. Lempel and J. Ziv, On the complexity of finite sequences, IEEE Transactions on Information Theory 22, 75 (1976).

[8]

J.-L. Blanc, L. Pezard, and A. Lesne, Delay independence of mutual-information rate of two symbolic sequences, Phys. Rev. E 84, 036214 (2011).

[9]

S. Zozor, P. Ravier, and O. Buttelli, On lempel–ziv complexity for multidimensional data analysis, Physica A: Statistical Mechanics and Its Applications 345, 285 (2005).

[10]

E. Estevez-Rams, R. Lora Serrano, B. Aragón Fernández, and I. Brito Reyes, On the non-randomness of maximum Lempel Ziv complexity sequences of finite size, Chaos: An Interdisciplinary Journal of Nonlinear Science 23, 023118 (2013).

[11]

R. Giglio, R. Matsushita, A. Figueiredo, I. Gleria, and S. D. Silva, Algorithmic complexity theory and the relative efficiency of financial markets, Europhysics Letters 84, 48005 (2008).

[12]

C. Taufemback, R. Giglio, and S. D. Silva, Algorithmic complexity theory detects decreases in the relative efficiency of stock markets in the aftermath of the 2008 financial crisis, Economics Bulletin 31, 1631 (2011).

[13]

R. Giglio and S. Da Silva, Ranking the Stocks Listed on Bovespa According to Their Relative Efficiency, MPRA Paper, University Library of Munich, Germany, 2009.

[14]

Y. Bai, Z. Liang, and X. Li, A permutation lempel-ziv complexity measure for EEG analysis, Biomedical Signal Processing and Control 19, 102 (2015).

[15]

M. Borowska, Multiscale permutation lempel–ziv complexity measure for biomedical signal analysis: Interpretation and application to focal EEG signals, Entropy 23, (2021).

[16]

B. K. Hillen, G. T. Yamaguchi, J. J. Abbas, and R. Jung, Joint-specific changes in locomotor complexity in the absence of muscle atrophy following incomplete spinal cord injury, Journal of NeuroEngineering and Rehabilitation 10, 1 (2013).

[17]

M. D. Costa, C.-K. Peng, and A. L. Goldberger, Multiscale analysis of heart rate dynamics: Entropy and time irreversibility measures, Cardiovascular Engineering 8, 88 (2008).

[18]

R. A. Fisher and E. J. Russell, On the mathematical foundations of theoretical statistics, Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 222, 309 (1922).

[19]

B. Hjorth, EEG analysis based on time domain properties, Electroencephalography and Clinical Neurophysiology 29, 306 (1970).

[20]

F. Mormann, T. Kreuz, C. Rieke, R. G. Andrzejak, A. Kraskov, P. David, C. E. Elger, and K. Lehnertz, On the predictability of epileptic seizures, Clinical Neurophysiology 116, 569 (2005).

[21]

V. Marmelat, K. Torre, and D. Delignieres, Relative roughness: An index for testing the suitability of the monofractal model, Frontiers in Physiology 3, (2012).

[22]

T. M. Cover, Elements of Information Theory (John Wiley & Sons, 1999).

[23]

A. Hacine-Gharbi and P. Ravier, A binning formula of bi-histogram for joint entropy estimation using mean square error minimization, Pattern Recognition Letters 101, 21 (2018).